Математика.
5 клас. Формуємо і перевіряємо предметні компетентності.
Вправи. Самостійні
роботи. Тематичні
контрольні роботи. Завдання для експрес-контролю.
Схвалено для використання в освітньому процесі
Протокол №11засідання експертної
комісії з математики
від 28.11.2022, зареєстрований у каталозі надання грифів навчальній
літературі та навчальним програмам
за № 3.0651-2022
Купити
книгу, скориставшись послугой
«КНИГА—ПОШТОЮ».
Попередня книга
Наступна книга
ПЕРЕДМОВА
Посібник
містить дидактичні матеріали
з курсу математики 5-го класу відповідно до модельної
навчальної програми
(автор Істер О. С.): 1498 вправ
за основними темами
та 67 — за додатковими, 19 рівневих
самостійних
робіт, кожну з яких подано в 6 варіантах (три рівні по два
рівноцінних
варіанти); 10 діагностичних (контрольних) робіт та контрольну
роботу за рік,
кожну з яких подано у двох рівноцінних варіантах та 10 наборів
завдань для
проведення рівневого
експрес-контролю знань (кожен у
двох варіантах).
Для
зручності користування
посібником у назві кожної самостійної роботи, діагностичної
(контрольної)
роботи чи завдання для експрес-контролю знань зазначено
відповідну тему.
Наприкінці посібника є відповіді та поради до більшості вправ.
До самостійних,
діагностичних, контрольної роботи за рік та завдань для
експрес-контролю знань
відповіді відсутні. Тому вчитель, придбавши посібник на весь
клас (або один
примірник на парту), може використовувати його під час
будь-якого уроку
(закріплення нових знань, перевірки знань, експрес-контролю
знань тощо).
Розглянемо
деякі особливості посібника
та роботи з ним.
1. Вправи. Посібник містить вправи для робіт у класі
та вдома. Номери
вправ, рекомендованих для виконання вдома, позначено на
темному тлі. Задачі,
позначені кружечком (°), відповідають початковому та
середньому рівням
навчальних досягнень; задачі без цієї позначки — достатньому
та високому рівням
навчальних досягнень. Достатня кількість вправ дасть змогу
вчителю використовуватиьпосібник
майже щоуроку
та задавати по ньому домашні завдання.
2. Самостійні роботи. У посібнику подано добірку рівневих
самостійних робіт. Їх позначено півжирною
буквою з
відповідним номером. Після номера вказано одну з літер А, Б
або В (наприклад, С–2Б),
що означає:
А
— самостійна
робота, що відповідає початковому та
середньому рівням навчальних досягнень;
Б — самостійна робота, що відповідає достатньому рівню
навчальних досягнень;
В — самостійна робота, що відповідає високому рівню навчальних
досягнень.
Для
кожного рівня подано два
рівноцінних варіанти.Кожна
самостійна робота містить
3 завдання і розрахована на 15–30 хв (залежно від теми).
Самостійні роботи
мають
зазвичай навчальний характер і не призначені для оцінювання
знань учнів. Якщо
вчитель захоче оцінити роботу, то за кожне завдання рівня А
автор пропонує
нараховувати
по 2 бали, рівня Б — 3 бали, рівня В — 4 бали. Отже,
максимальна оцінка за
роботу рівня А — 6 балів, рівня Б — 9 балів, рівня В — 12
балів. Під час
оцінювання кожного завдання вчитель може застосовувати
систему, подану нижче
(для оцінювання тематичної контрольної
роботи). Рівень самостійної роботи, що виконує учень, зазвичай
визначає
вчитель.
3. Діагностичні (контрольні) роботи (ДР). Кожна
ДР містить
завдання, що відповідають початковому і середньому рівням
навчальних досягнень
(їх позначено кружечками), та завдання, що відповідають
достатньому і високому
рівням навчальних досягнень. Усі завдання оцінено в балах так,
що максимальна
оцінка за ДР дорівнює 12 балам. Кожна ДР розрахована на один
урок (45 хв).
Залежно
від рівня підготовленості
учнів класу та їхніх індивідуальних
особливостей
учитель може зменшити кількість завдань у кожній ДР, змінюючи
при
цьому кількість
балів за деякі завдання так, щоб сума балів дорівнювала 12.
Автор
пропонує на першому етапі вести
оцінювання кожного завдання у звичній для вчителя математики
системі
«плюс—мінус»:
«+» (плюс) — учень повністю розв’язав завдання;
«±» (плюс—мінус) — хід розв’язування завдання правильний, але
допущено помилки
логічного або обчислювального характеру, які призвели до
неправильної
відповіді;
«
» (мінус—плюс) —
розв’язування
завдання не закінчено, але учень суттєво наблизився до
повного розв’язання,
виконавши, не менше від його половини;
«–» (мінус) —
учень почав розв’язувати правильно (наприклад, зробив малюнок,
записав фрагмент
розв’язання),
але виконав завдання менше ніж наполовину;
«0» (нуль) — учень не починав завдання або почав неправильно.
На другому етапі вчитель переводить оцінку із системи
«плюс—мінус» у бали.
Пропонуємо таку шкалу.
|
Максимальний
бал за завдання |
Оцінки
в системі “плюс-мінус”. Переведення
в бали |
|||
|
+ |
± |
|
– |
|
|
1 |
1 |
0,5 |
0,5 |
0 |
|
2 |
2 |
1,5 |
1 |
0,5 |
|
3 |
3 |
2–2,5 |
1–1,5 |
0,5 |
|
4 |
4 |
3 |
2 |
1 |
Оцінкою за роботу є сума балів, яку отримав учень
за виконання
кожного завдання окремо. Якщо сумою
є не ціле число (а саме — це число має п’ять десятих), то
користуємося звичним
правилом округлення (наприклад, 9,5 ≈ 10).
Безумовно,
учитель може
використовувати більш просту, інтуїтивно зрозумілу для учнів
систему оцінювання
кожного завдання: якщо учень отримав правильну відповідь і
навів повне її
обґрунтування, то завдання оцінюється максимальною кількістю
балів; якщо учень
навів окремі етапи правильного розв’язання завдання, то —
кількістю балів,
меншою від максимально можливої за це завдання.
Відповідно
до рекомендацій щодо
оцінювання результатів навчання учнів 5–6 класів, які
здобувають освіту
відповідно до нового Державного стандарту базової середньої
освіти, затвердженого наказом Міністерства освіти і науки
України № 289 від 1
квітня 2022 р. (Додаток 1), у свідоцтво досягнень учня/учениці
вносяться характеристики
результатів навчальної діяльності (таблиця 1).
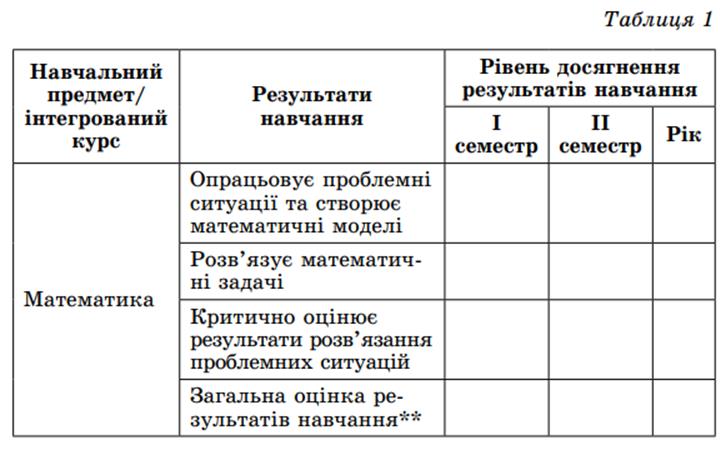
Розглянемо, як оцінювати результати за кожною із
цих
характеристик.
На думку автора, учитель не матиме проблем із
оцінюванням такої
складової результатів навчання, як уміння розв’язувати
математичні задачі.
А от для того, щоб учителю було легше визначитися
з оцінюванням
уміння опрацьовувати проблемні ситуації та створювати
математичні моделі,
автор у кожній діагностичній роботі виокремив по кілька вправ
(їхні номери
підкреслено), які мають допомогти оцінити цей результат
навчання. До таких
завдань автор зарахував текстові задачі, завдання з
логічним
навантаженням, на встановлення
закономірностей, на встановлення відповідності («логічні
пари») тощо.
Остаточний вибір переліку вправ для кожної письмової роботи,
за якими вчитель
оцінюватиме цей результат навчання, залишається за педагогом.
Таку
характеристику, як критичне оцінювання
результатів розв’язання проблемних ситуацій, автор
пропонує оцінювати після
виконання кожної письмової роботи на основі рефлексії учнів.
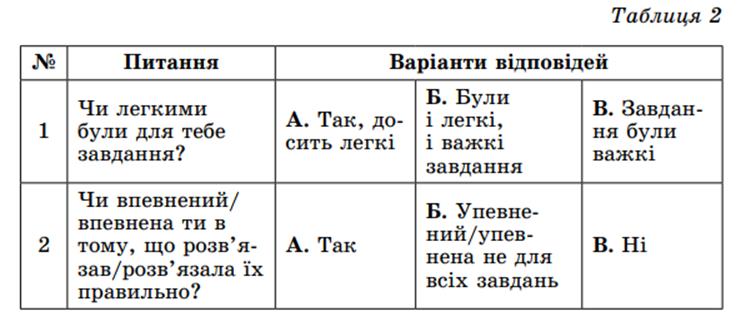
Наприклад, після
виконання письмової роботи можна запропонувати учням просте
анкетування, яке
дозволить з’ясувати в кожного з них, наскільки легкою/важкою
була для нього
робота та чи впевнений він/вона у правильності розв’язування
вправ. Можливий
варіант такого анкетування наведено в таблиці 2. Діти мають
дати відповідь у
форматі, наприклад, «1–Б», «2–В», а вчитель, зіставивши оцінку
за діагностичну
роботу та результат самооцінювання
учня, зможе
орієнтовно визначити, наскільки учень критично оцінює
результати розв’язання
проблемних ситуацій
4. Завдання для
експрес-контролю знань (ЕК). Якщо учень пропустив
урок, на якому
проводилася ДР, йому можна запропонувати рівневі завдання для
ЕК. Автор
пропонує
вчителю спочатку визначити середню поточну оцінку учня,яка
враховує відповіді біля дошки, ведення зошита тощо;а
потім запропонувати учневі завдання ЕК на один рівень
вищий за рівень середньої поточної оцінки. Кожен з рівнів, що
відповідає рівням
навчальних досягнень (середньому, достатньому та високому),
має завдання, сума
балів за які дорівнює «3». Кожне завдання вчитель оцінює в
системі «плюс—мінус»,
а потім переводить у бали (див.
табл. вище).
Якщо
під час ЕК учень бездоганно
виконав завдання середнього чи достатнього рівня, то вчитель
може запропонувати
йому завдання більш високого рівня.
Сума
середньої поточної оцінки та
балів, набраних під час
ЕК, учитель може
враховувати під час виставлення оцінки за тему як оцінку, яку
отримали інші
учні під час
ДР, або якимось іншим чином на власний розсуд.
Зичимо
успіхів!